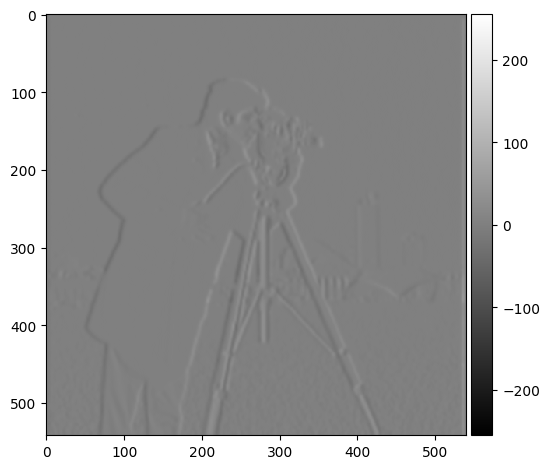
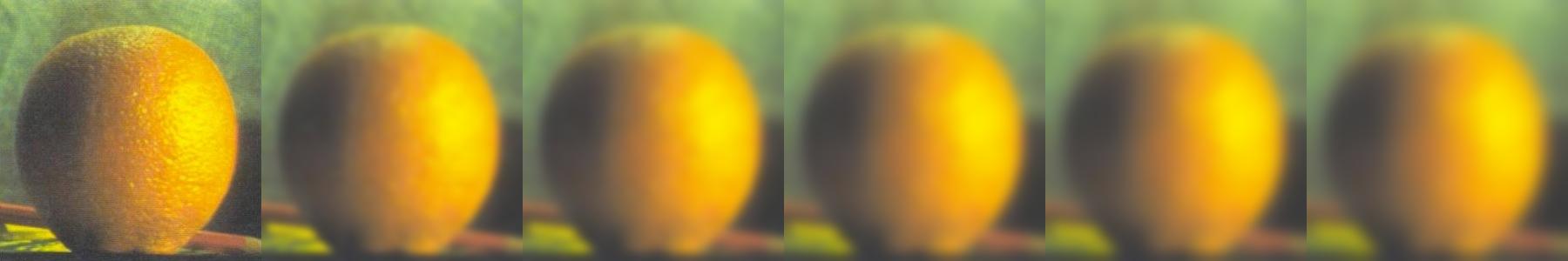partial derivative dx

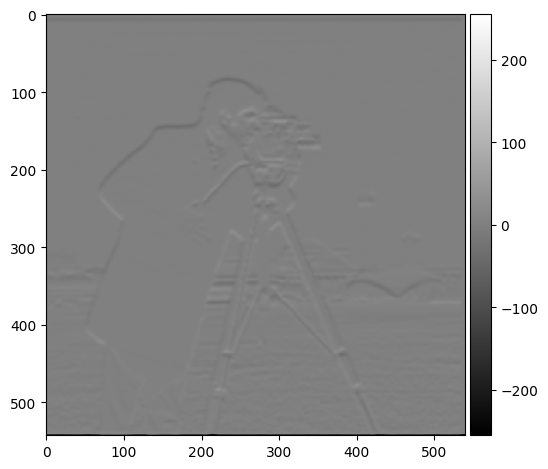
partial derivative dy

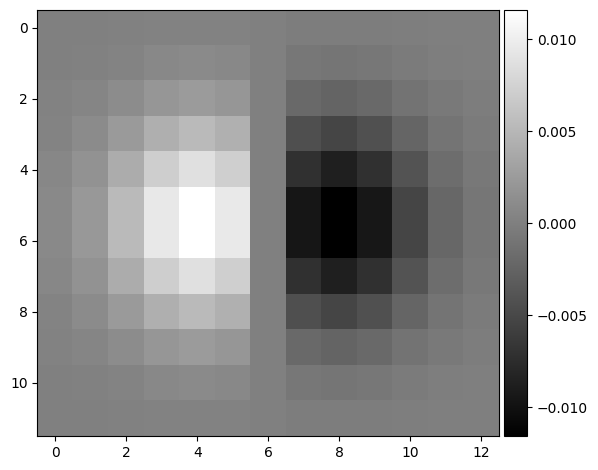
gradient magnitude
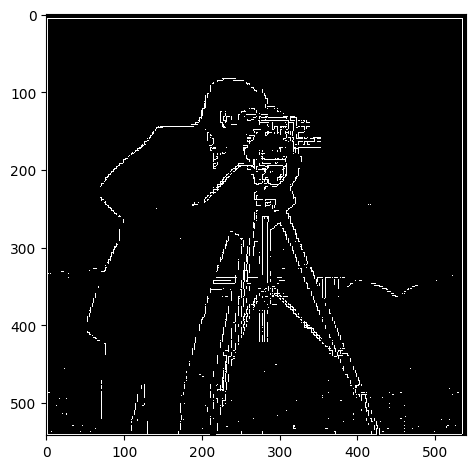
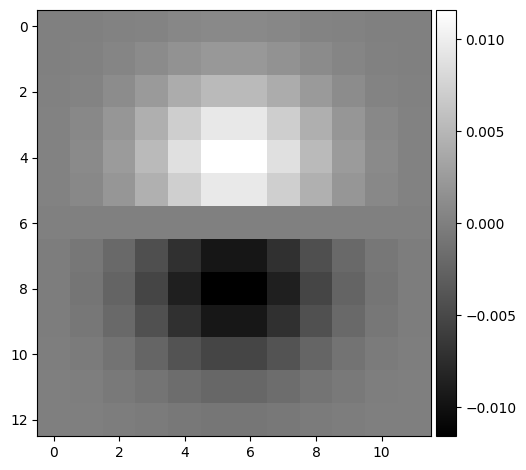
gradient magnitude binarized
For this project, my task was to color these photographs originally captured by Prokudin-Gorskii. My strategy for this was to take the same photograph with blue, green, and red color filters and then stack the photos on top of each other to create a fully-colored image.